# load packages
library(tidyverse)
library(tidymodels)
library(colorspace)
library(cowplot)
library(distributional)
library(emmeans)
library(gapminder)
library(ggdist)
library(margins)
library(ungeviz) # install_github("wilkelab/ungeviz")
# set theme for ggplot2
ggplot2::theme_set(ggplot2::theme_minimal(base_size = 16))
# set figure parameters for knitr
knitr::opts_chunk$set(
fig.width = 7, # 7" width
fig.asp = 0.618, # the golden ratio
fig.retina = 3, # dpi multiplier for displaying HTML output on retina
fig.align = "center", # center align figures
dpi = 300 # higher dpi, sharper image
)Visualizing uncertainty I
Lecture 16
Duke University
STA 313 - Spring 2024
Warm up
Announcements
- Project 2 proposals due by 1 pm tomorrow
- Peer review of proposals in lab
Setup
Probability
Let’s imagine we’re playing a game
The odds are in your favor:
You have a 90% chance of winning!
playing…
Sorry, you lost. 😞
How does that make you feel?
We are bad at judging uncertainty
You had a 10% chance of losing
One in ten playing this game will lose
90% chance of winning is nowhere near a certain win
It helps to visualize a set of possible outcomes
Possible outcomes from 100 individual games played
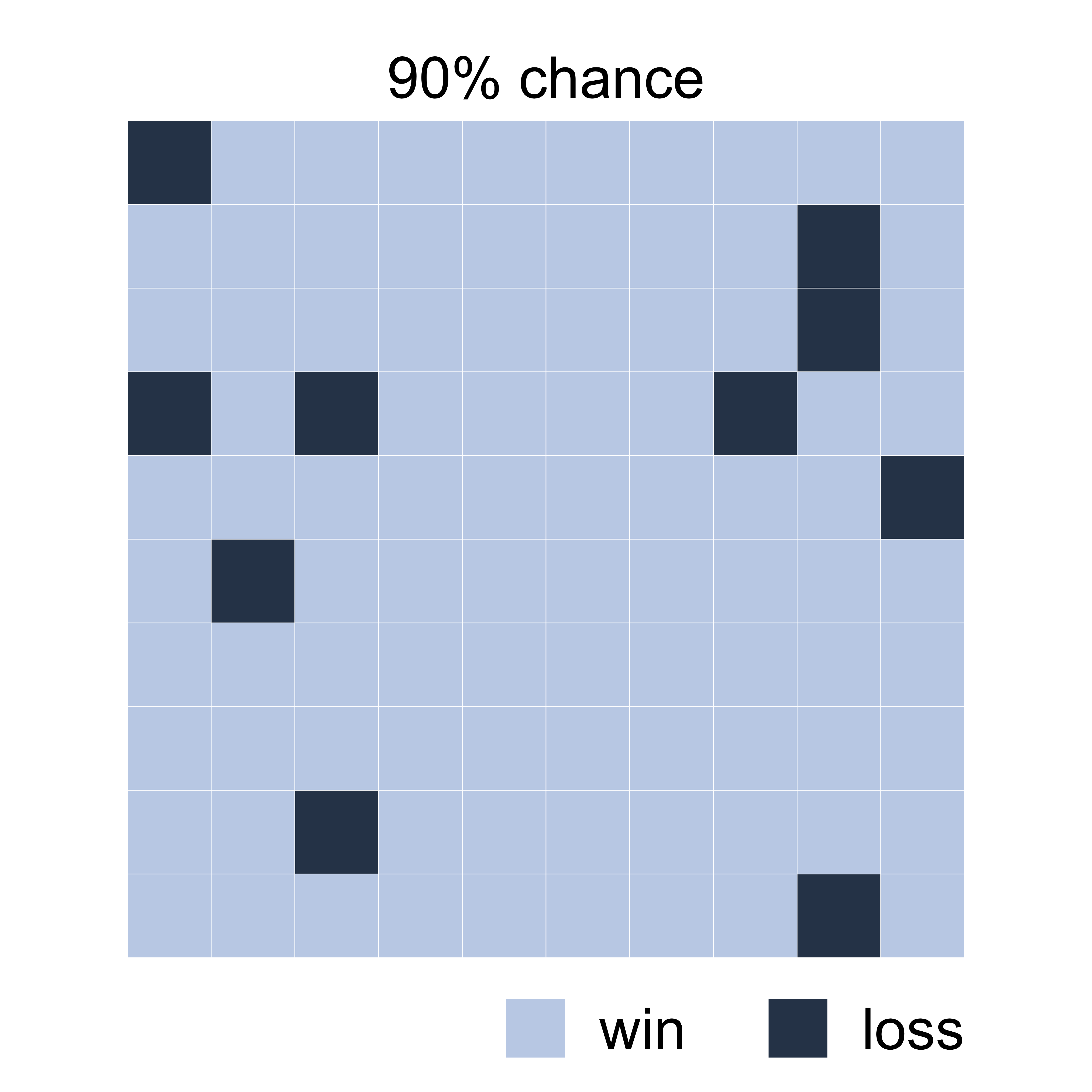
Frequency framing
This type of visualization is called frequency framing
Uncertainty
Visualizing uncertainty of point estimates
- A point estimate is a single number, such as a mean
- Uncertainty is expressed as standard error, confidence interval, or credible interval
- Important: Uncertainty of a point estimate != variation in the sample
Key concepts of statistical sampling
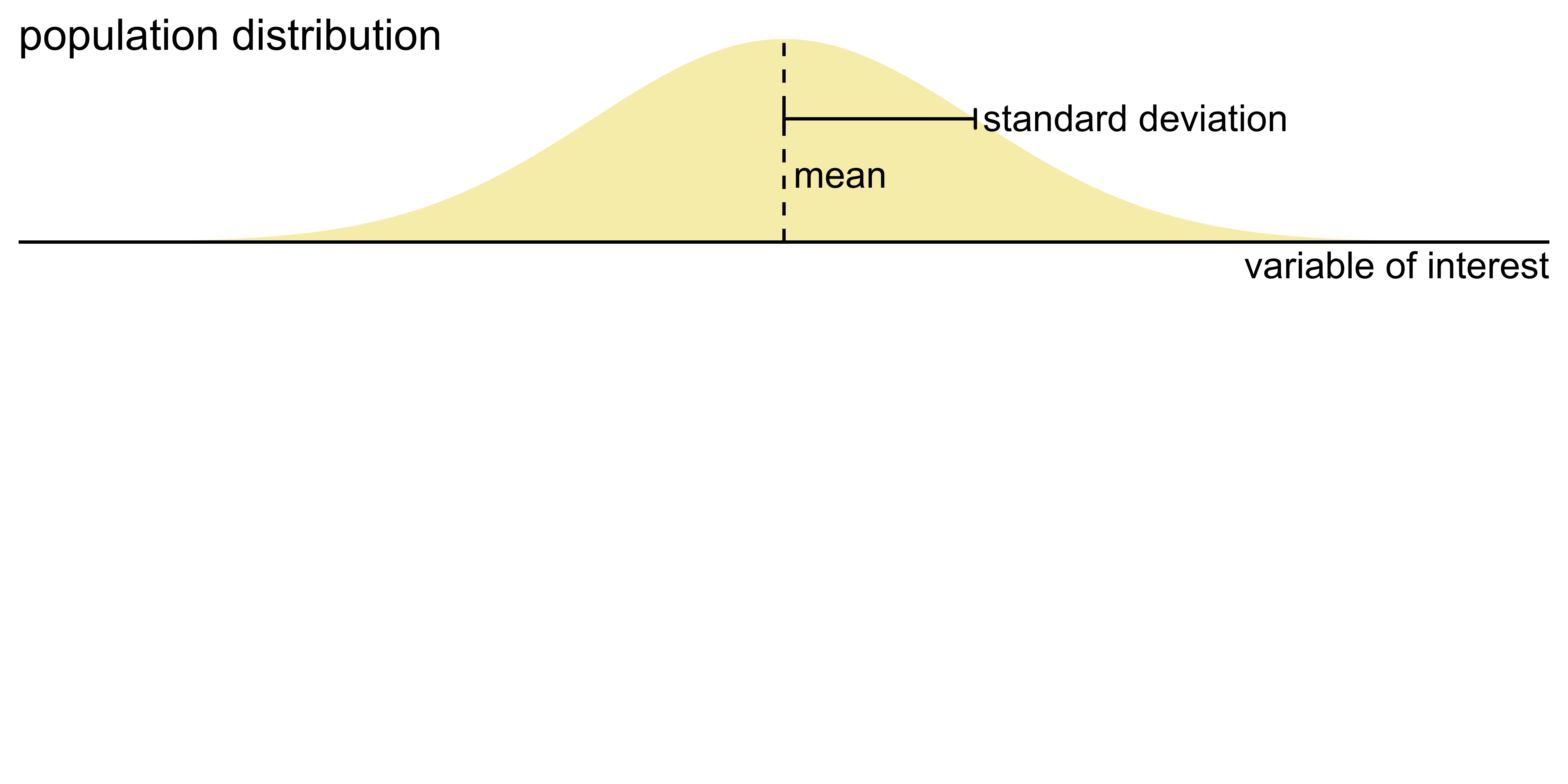
Key concepts of statistical sampling
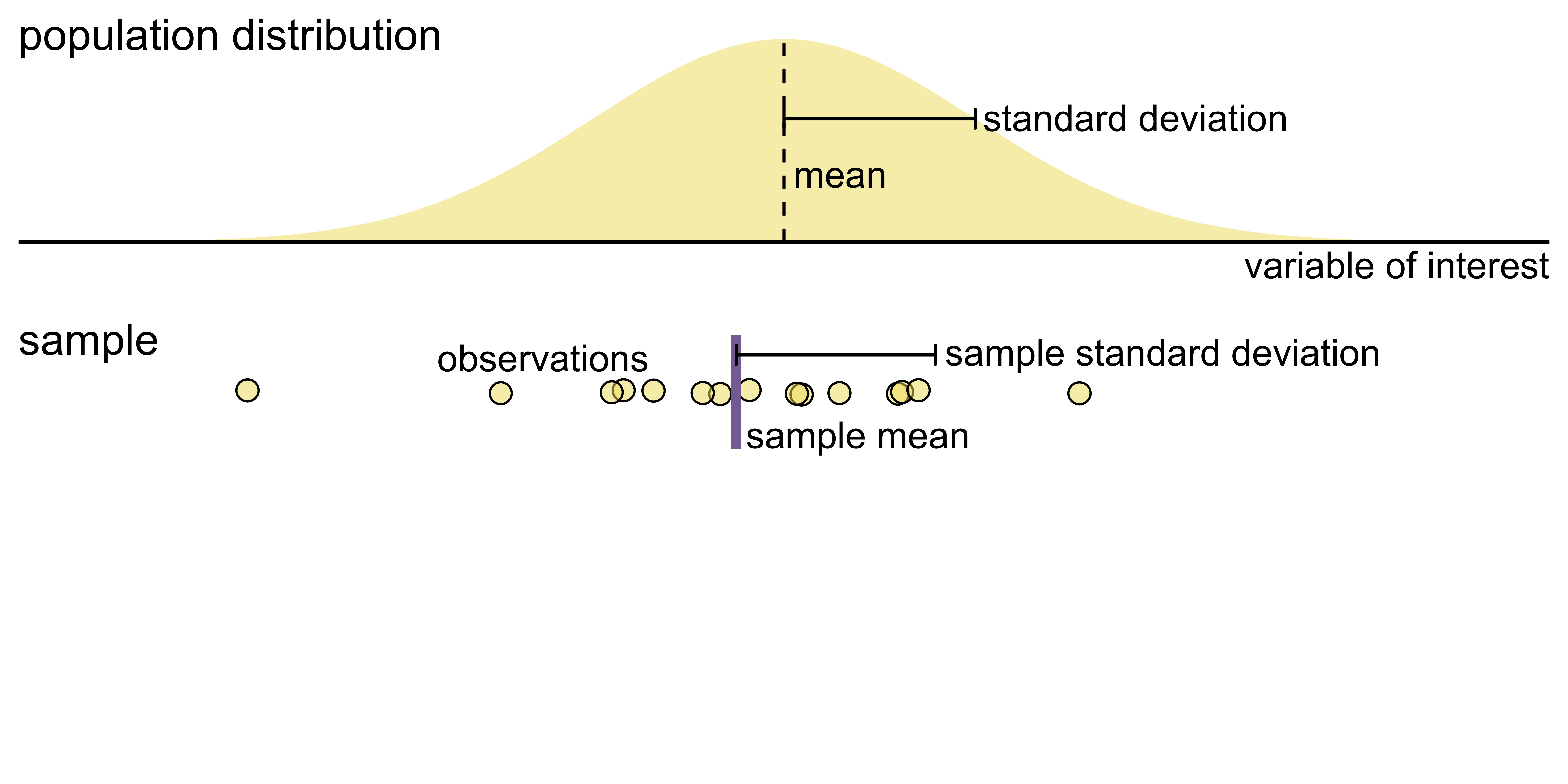
Key concepts of statistical sampling
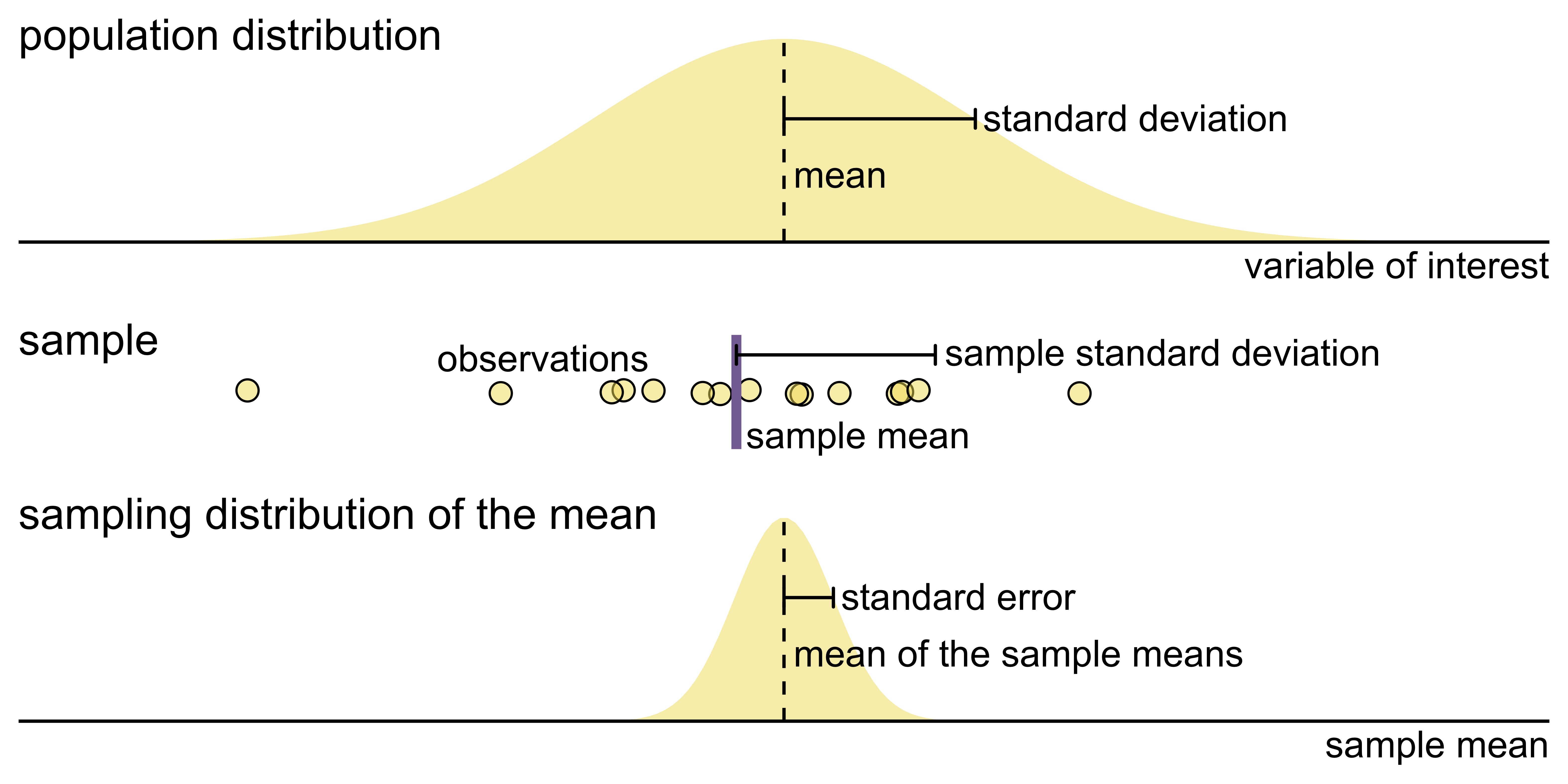
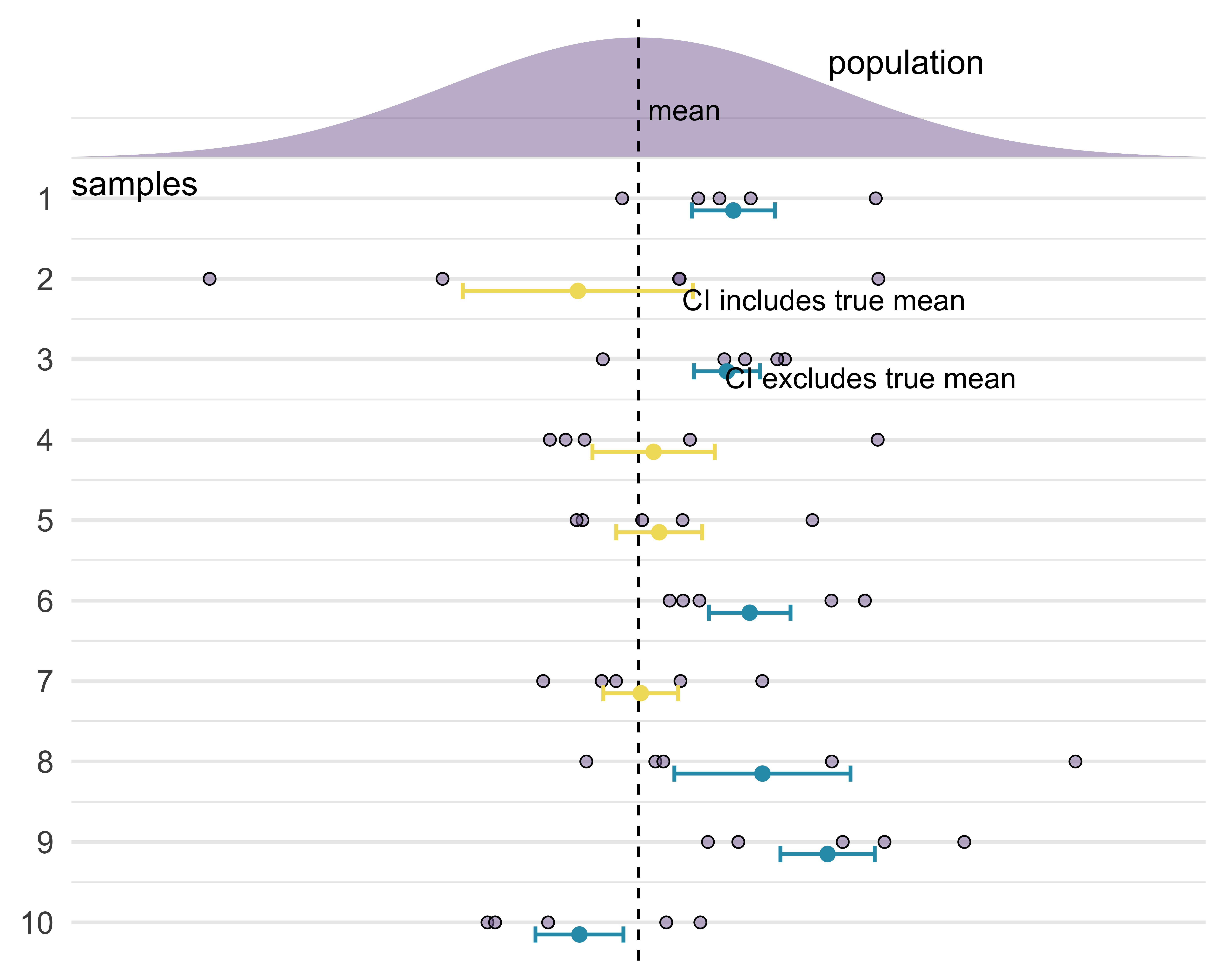
Confidence intervals
What does “95% confident” mean in the following sentence?
Frequentist interpretation of a confidence interval
Everest
# A tibble: 21,813 × 21
expedition_id member_id peak_id peak_name year season sex age
<chr> <chr> <chr> <chr> <dbl> <chr> <chr> <dbl>
1 EVER63101 EVER63101-03 EVER Everest 1963 Spring M 36
2 EVER63101 EVER63101-04 EVER Everest 1963 Spring M 31
3 EVER63101 EVER63101-05 EVER Everest 1963 Spring M 27
4 EVER63101 EVER63101-06 EVER Everest 1963 Spring M 26
5 EVER63101 EVER63101-07 EVER Everest 1963 Spring M 26
6 EVER63101 EVER63101-08 EVER Everest 1963 Spring M 29
7 EVER63101 EVER63101-01 EVER Everest 1963 Spring M 44
8 EVER63101 EVER63101-09 EVER Everest 1963 Spring M 37
9 EVER63101 EVER63101-10 EVER Everest 1963 Spring M 32
10 EVER63101 EVER63101-11 EVER Everest 1963 Spring M 26
# ℹ 21,803 more rows
# ℹ 13 more variables: citizenship <chr>, expedition_role <chr>, hired <lgl>,
# highpoint_metres <dbl>, success <lgl>, solo <lgl>, oxygen_used <lgl>,
# died <lgl>, death_cause <chr>, death_height_metres <dbl>, injured <lgl>,
# injury_type <chr>, injury_height_metres <dbl>Highest point reached on Everest in 2019
Includes only climbers and expedition members who did not summit
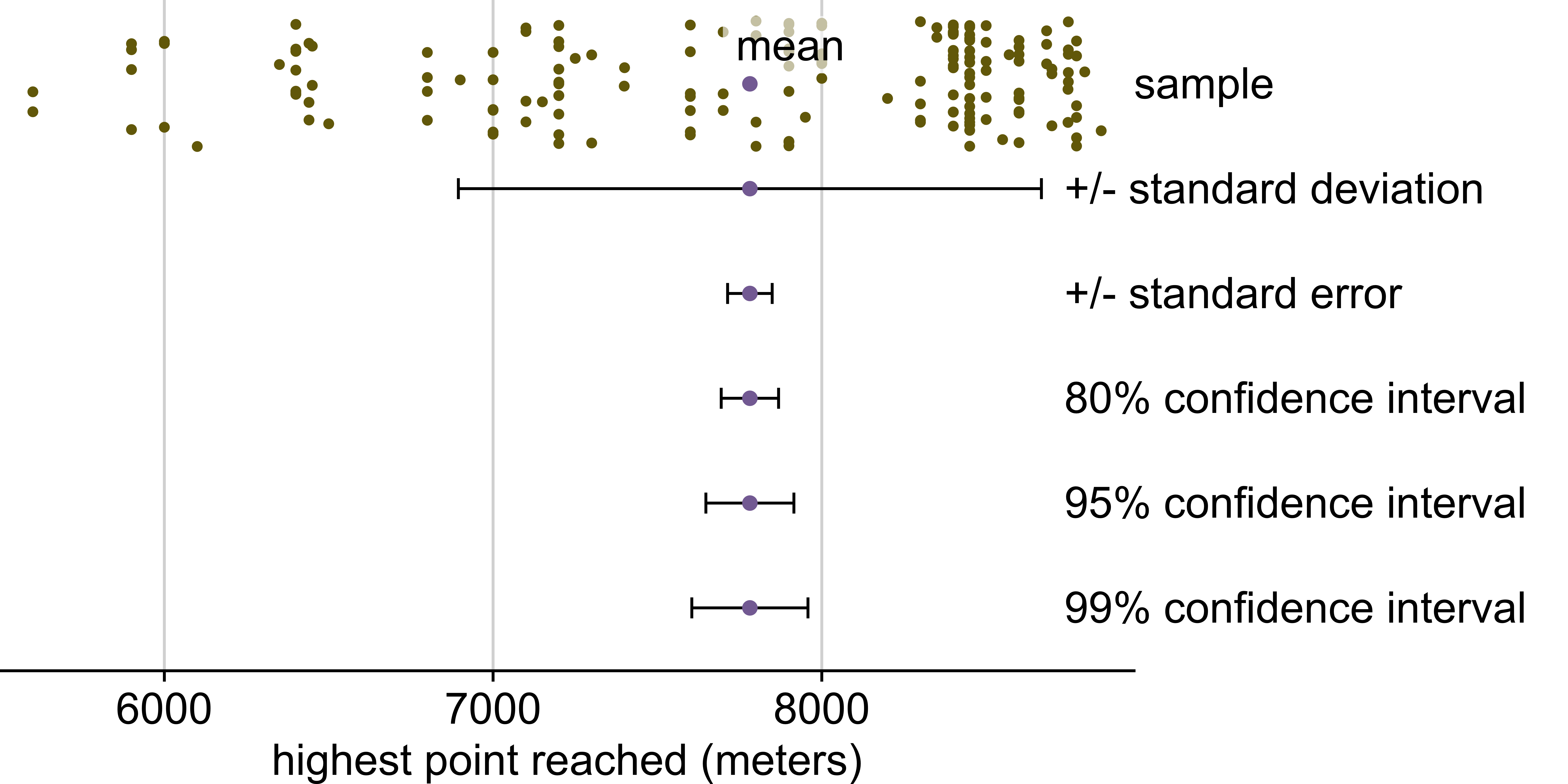
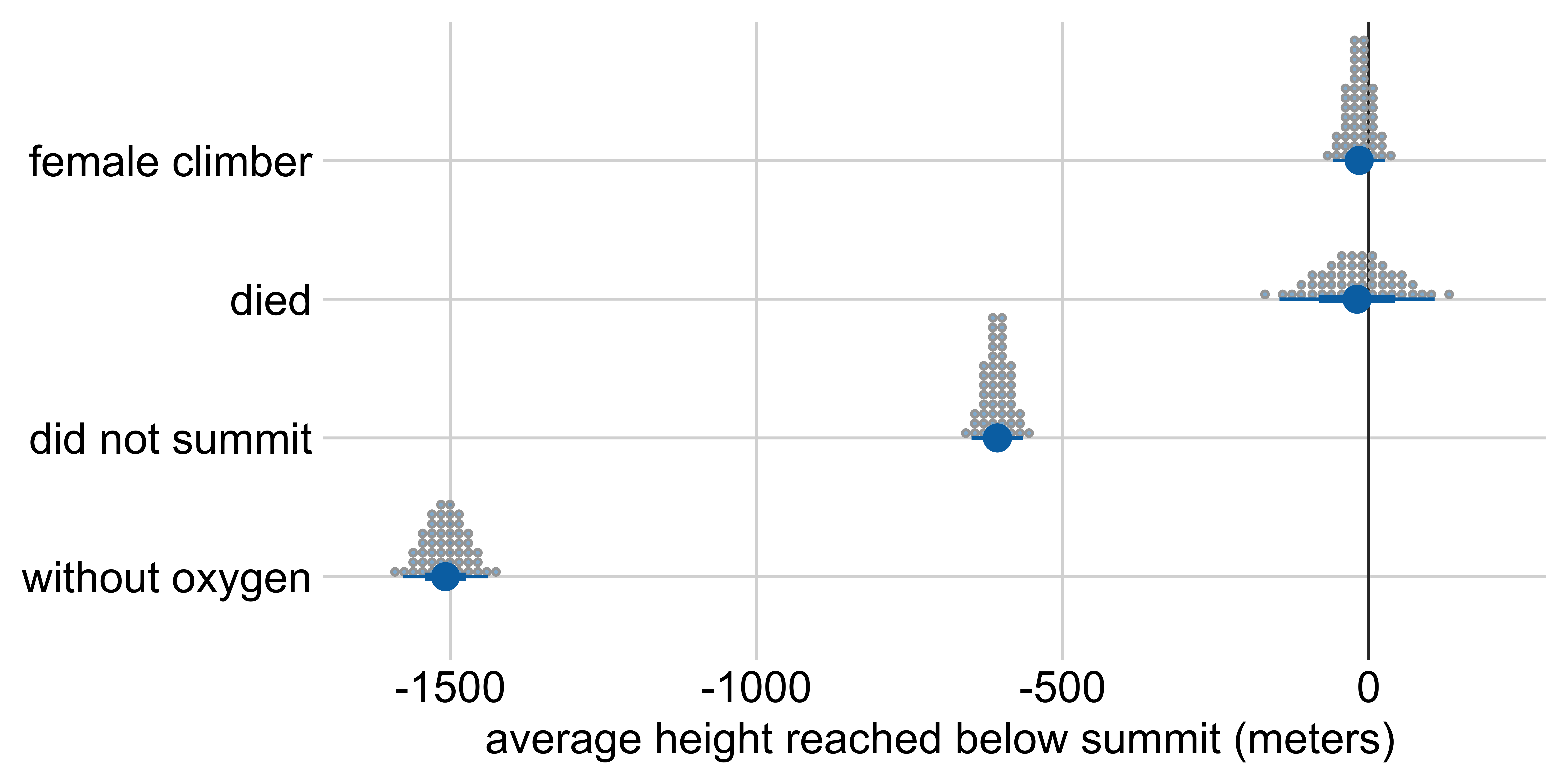
Marginal effects: Height reached on Everest
Average height reached relative to:
a male climber who climbed with oxygen, summited, and survived
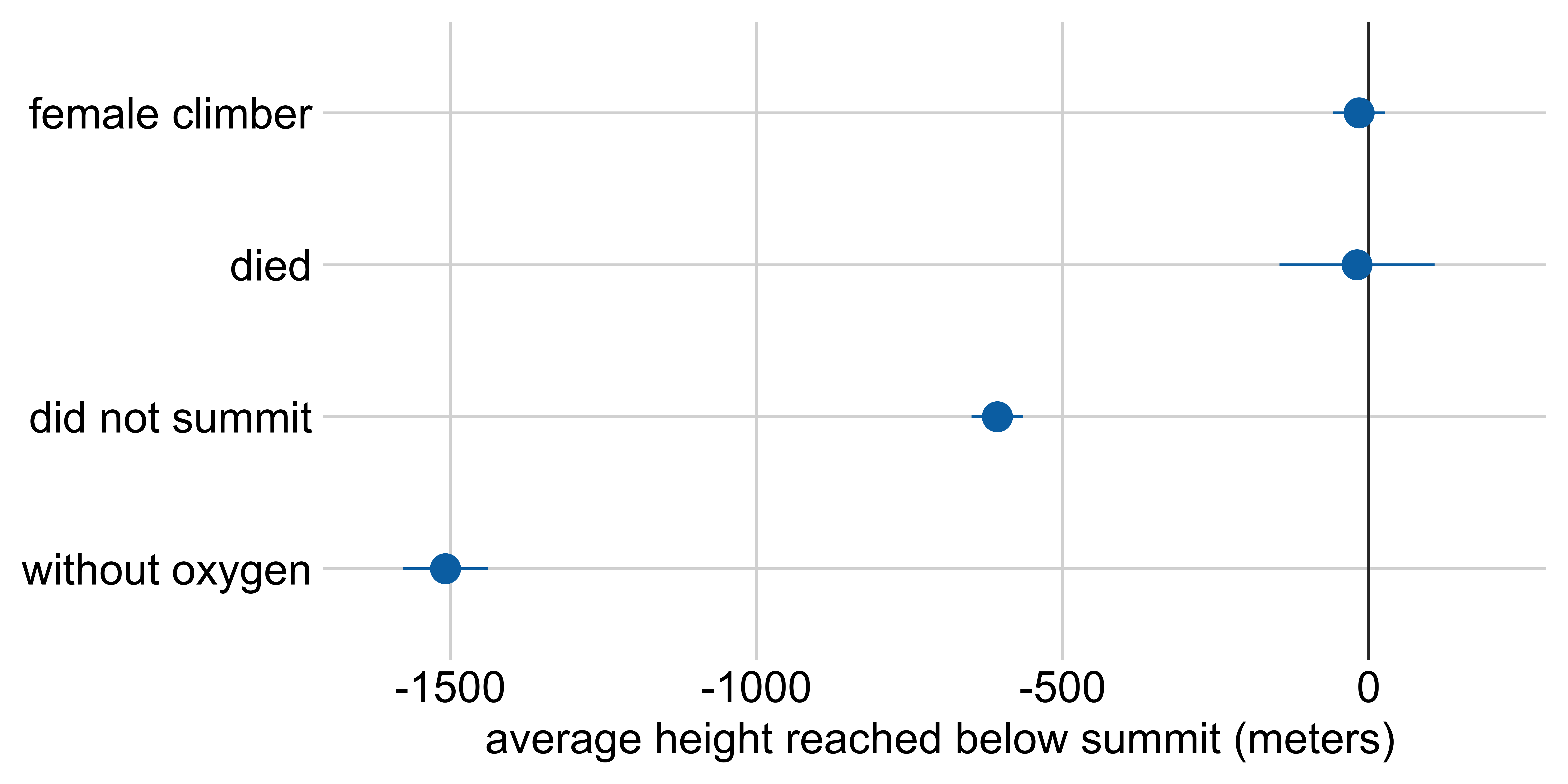
Marginal effects: Height reached on Everest
Other visualization options: half-eye
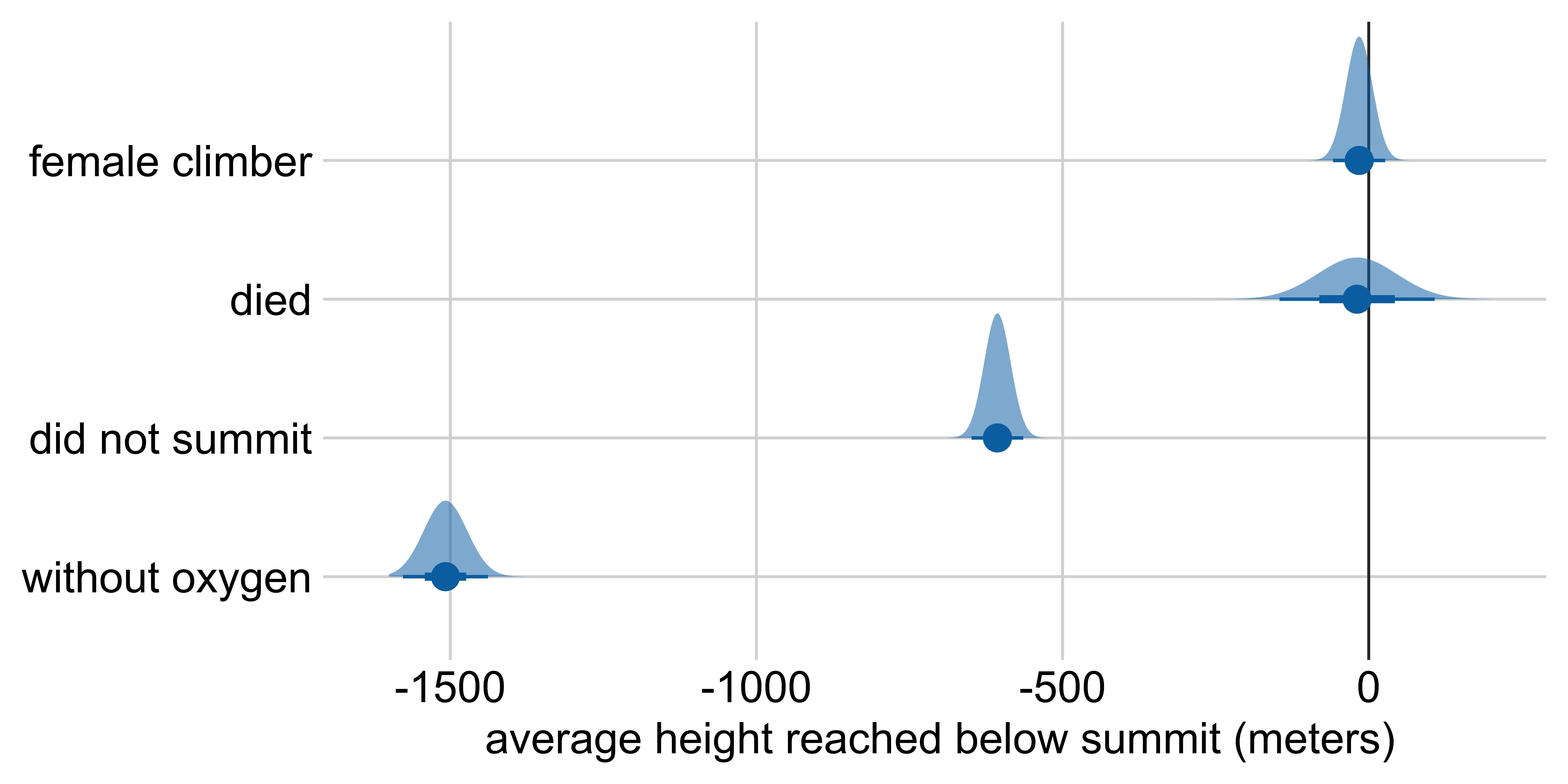
Marginal effects: Height reached on Everest
Other visualization options: gradient interval
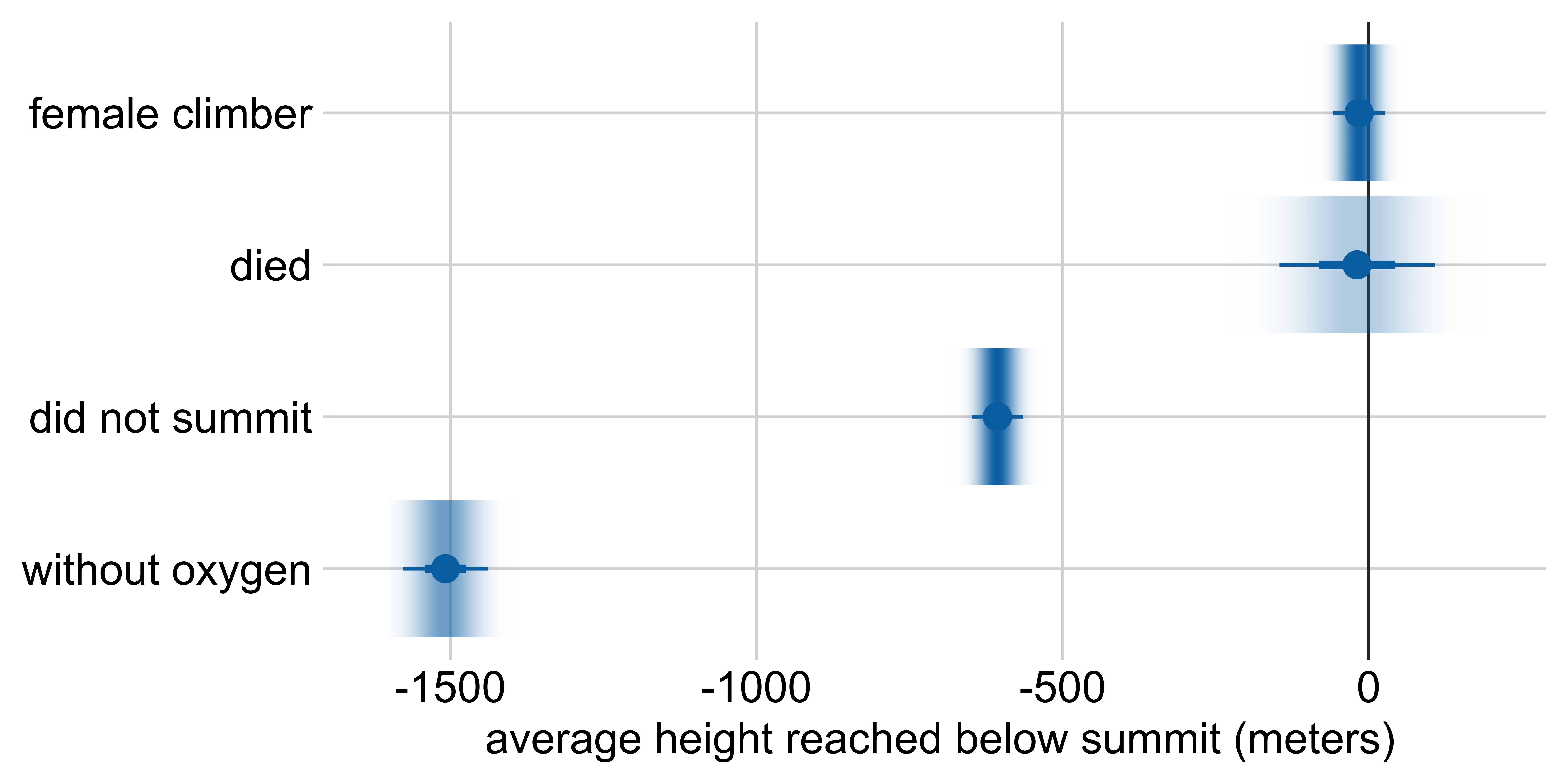
Marginal effects: Height reached on Everest
Other visualization options: quantile dotplot
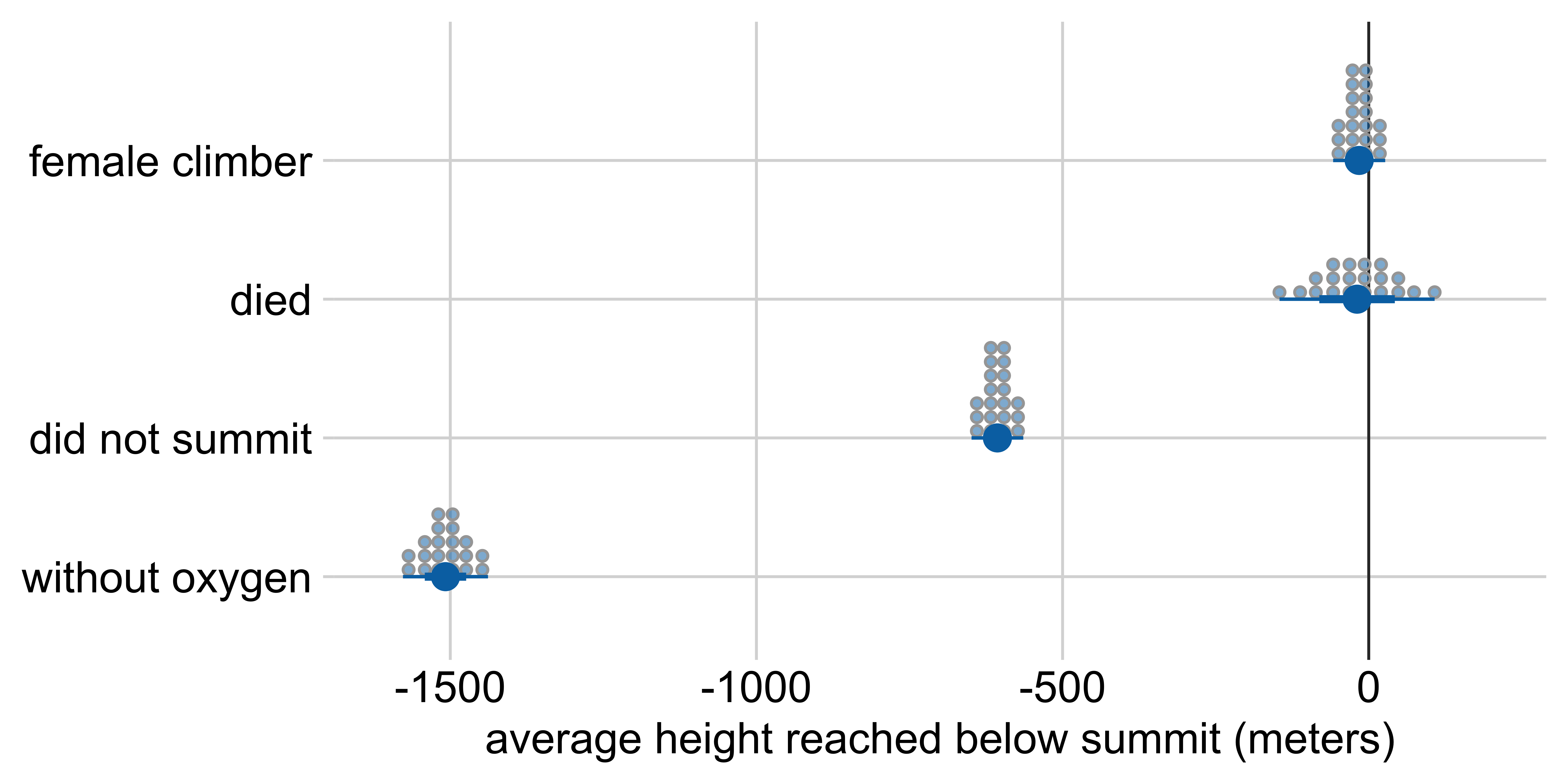
Marginal effects: Height reached on Everest
Other visualization options: quantile dotplot
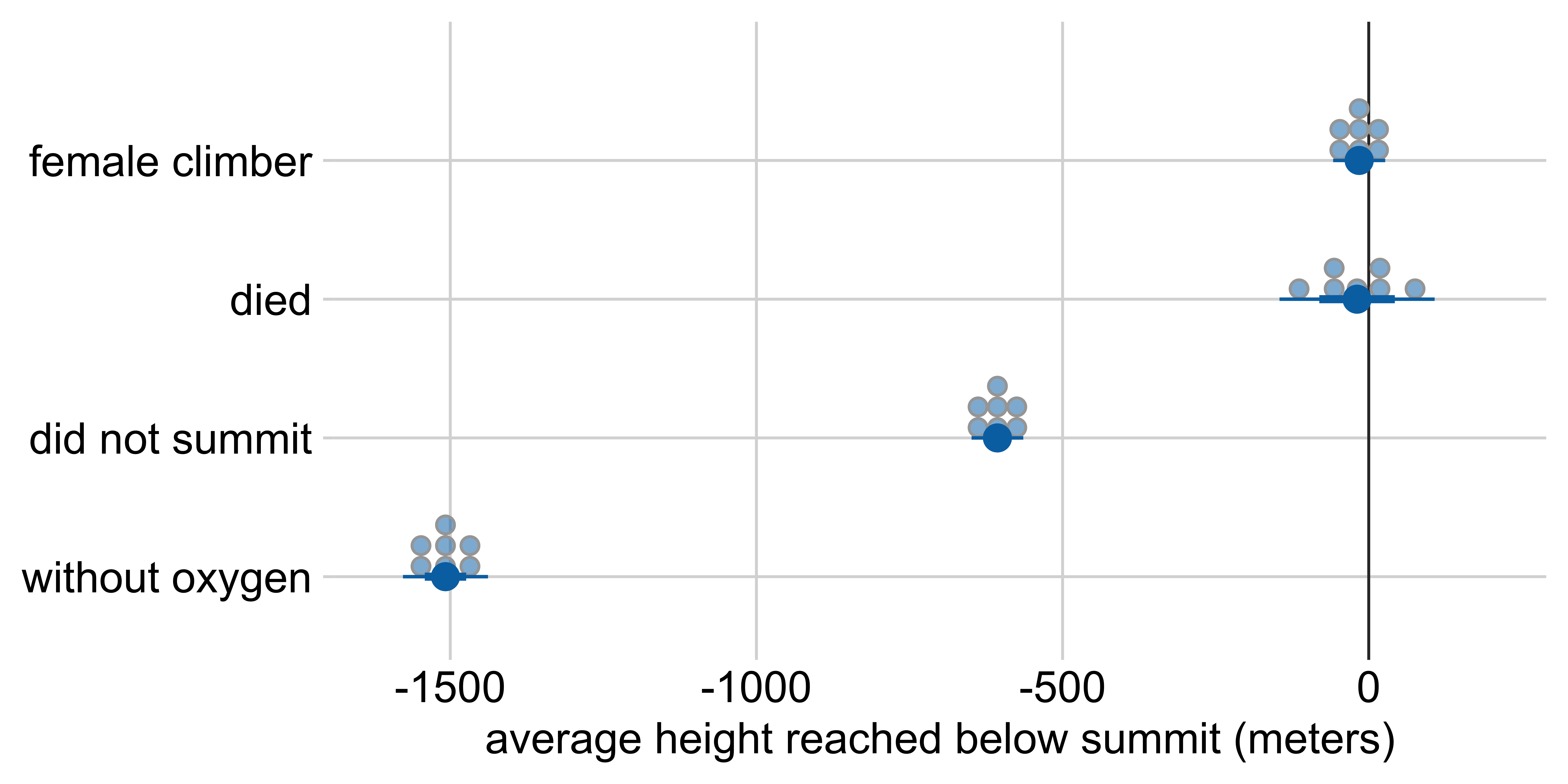
Marginal effects: Height reached on Everest
Other visualization options: quantile dotplot
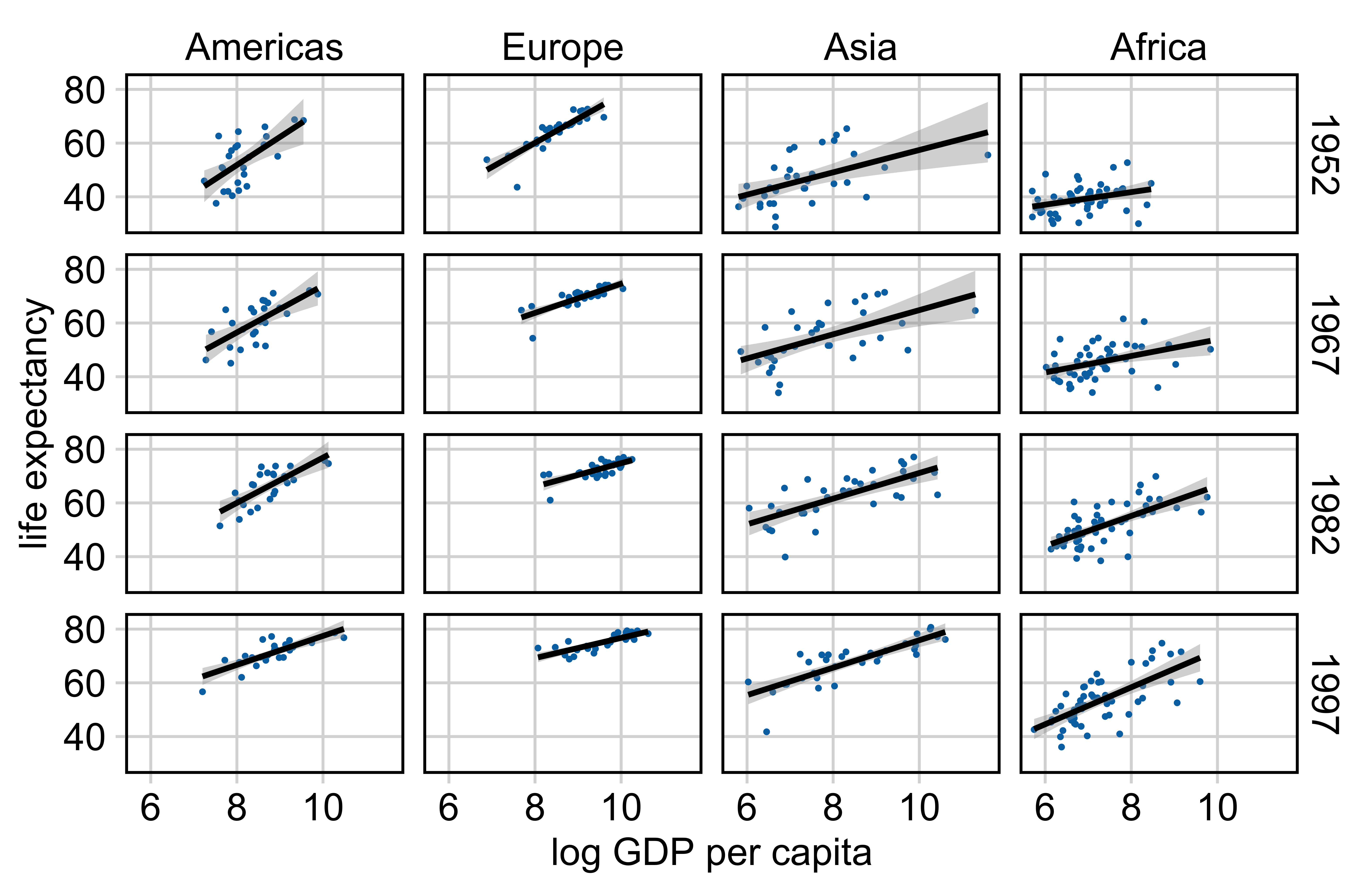
Making a plot with error bars in R
Example: Relationship between life expectancy and GDP per capita
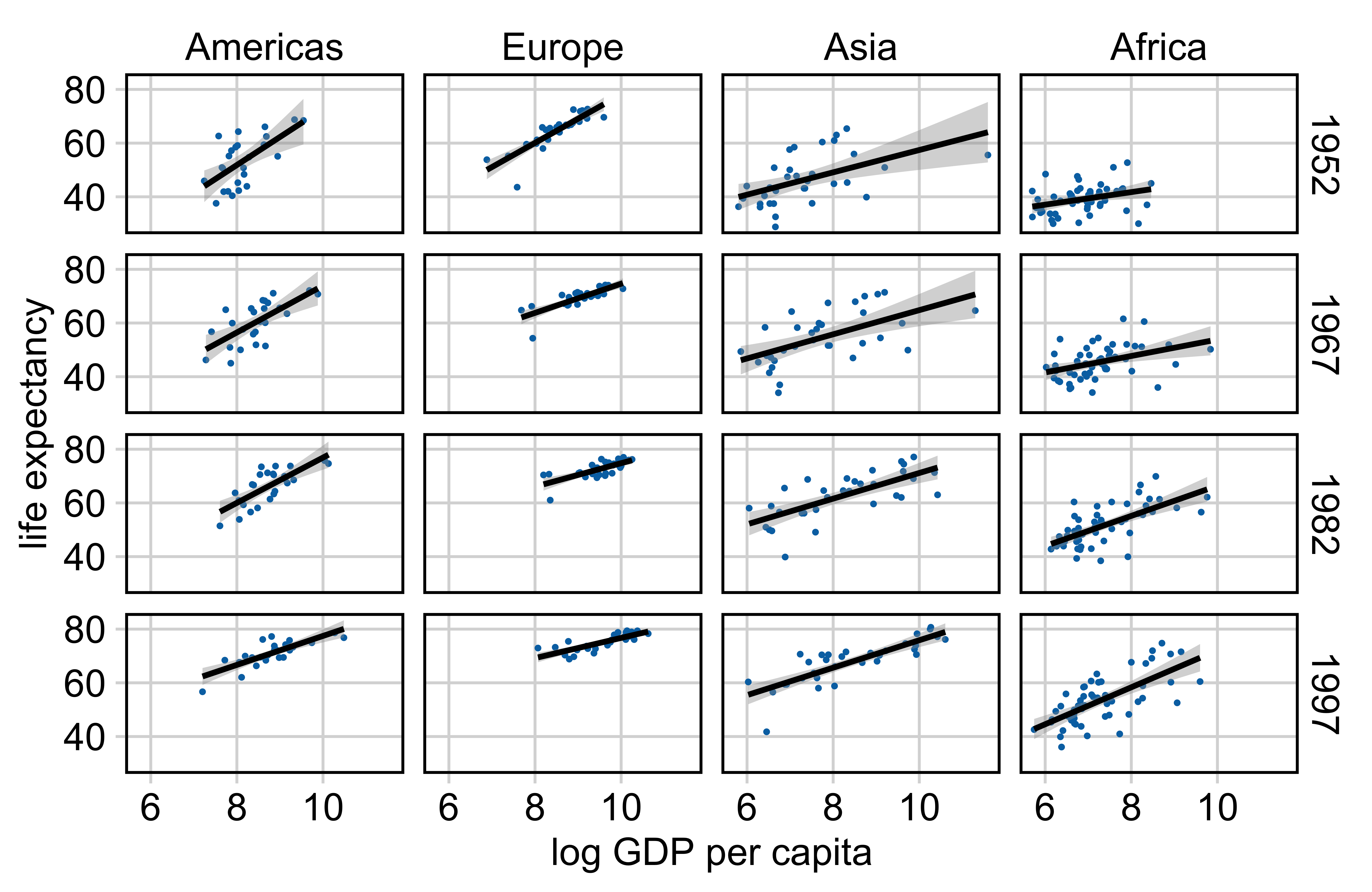
Making a plot with error bars in R
Example: Relationship between life expectancy and GDP per capita
Gapminder
See gapminder.org for fantastic visualizations and up-to-date data
# A tibble: 1,704 × 6
country continent year lifeExp pop gdpPercap
<fct> <fct> <int> <dbl> <int> <dbl>
1 Afghanistan Asia 1952 28.8 8425333 779.
2 Afghanistan Asia 1957 30.3 9240934 821.
3 Afghanistan Asia 1962 32.0 10267083 853.
4 Afghanistan Asia 1967 34.0 11537966 836.
5 Afghanistan Asia 1972 36.1 13079460 740.
6 Afghanistan Asia 1977 38.4 14880372 786.
7 Afghanistan Asia 1982 39.9 12881816 978.
8 Afghanistan Asia 1987 40.8 13867957 852.
9 Afghanistan Asia 1992 41.7 16317921 649.
10 Afghanistan Asia 1997 41.8 22227415 635.
# ℹ 1,694 more rowsMaking a plot with error bars in R
# A tibble: 60 × 3
continent year data
<fct> <int> <list>
1 Asia 1952 <tibble [33 × 4]>
2 Asia 1957 <tibble [33 × 4]>
3 Asia 1962 <tibble [33 × 4]>
4 Asia 1967 <tibble [33 × 4]>
5 Asia 1972 <tibble [33 × 4]>
6 Asia 1977 <tibble [33 × 4]>
7 Asia 1982 <tibble [33 × 4]>
8 Asia 1987 <tibble [33 × 4]>
9 Asia 1992 <tibble [33 × 4]>
10 Asia 1997 <tibble [33 × 4]>
# ℹ 50 more rowsMaking a plot with error bars in R
lm_data <- gapminder |>
nest(data = -c(continent, year)) |>
mutate(
fit = map(data, ~lm(lifeExp ~ log(gdpPercap), data = .x))
)
lm_data# A tibble: 60 × 4
continent year data fit
<fct> <int> <list> <list>
1 Asia 1952 <tibble [33 × 4]> <lm>
2 Asia 1957 <tibble [33 × 4]> <lm>
3 Asia 1962 <tibble [33 × 4]> <lm>
4 Asia 1967 <tibble [33 × 4]> <lm>
5 Asia 1972 <tibble [33 × 4]> <lm>
6 Asia 1977 <tibble [33 × 4]> <lm>
7 Asia 1982 <tibble [33 × 4]> <lm>
8 Asia 1987 <tibble [33 × 4]> <lm>
9 Asia 1992 <tibble [33 × 4]> <lm>
10 Asia 1997 <tibble [33 × 4]> <lm>
# ℹ 50 more rowsMaking a plot with error bars in R
lm_data <- gapminder |>
nest(data = -c(continent, year)) |>
mutate(
fit = map(data, ~lm(lifeExp ~ log(gdpPercap), data = .x)),
tidy_out = map(fit, tidy)
)
lm_data# A tibble: 60 × 5
continent year data fit tidy_out
<fct> <int> <list> <list> <list>
1 Asia 1952 <tibble [33 × 4]> <lm> <tibble [2 × 5]>
2 Asia 1957 <tibble [33 × 4]> <lm> <tibble [2 × 5]>
3 Asia 1962 <tibble [33 × 4]> <lm> <tibble [2 × 5]>
4 Asia 1967 <tibble [33 × 4]> <lm> <tibble [2 × 5]>
5 Asia 1972 <tibble [33 × 4]> <lm> <tibble [2 × 5]>
6 Asia 1977 <tibble [33 × 4]> <lm> <tibble [2 × 5]>
7 Asia 1982 <tibble [33 × 4]> <lm> <tibble [2 × 5]>
8 Asia 1987 <tibble [33 × 4]> <lm> <tibble [2 × 5]>
9 Asia 1992 <tibble [33 × 4]> <lm> <tibble [2 × 5]>
10 Asia 1997 <tibble [33 × 4]> <lm> <tibble [2 × 5]>
# ℹ 50 more rowsMaking a plot with error bars in R
lm_data <- gapminder |>
nest(data = -c(continent, year)) |>
mutate(
fit = map(data, ~lm(lifeExp ~ log(gdpPercap), data = .x)),
tidy_out = map(fit, tidy)
) |>
unnest(cols = tidy_out)
lm_data# A tibble: 120 × 9
continent year data fit term estimate std.error statistic p.value
<fct> <int> <list> <list> <chr> <dbl> <dbl> <dbl> <dbl>
1 Asia 1952 <tibble> <lm> (Interc… 15.8 9.27 1.71 9.78e-2
2 Asia 1952 <tibble> <lm> log(gdp… 4.16 1.25 3.33 2.28e-3
3 Asia 1957 <tibble> <lm> (Interc… 18.1 9.70 1.86 7.20e-2
4 Asia 1957 <tibble> <lm> log(gdp… 4.17 1.28 3.26 2.71e-3
5 Asia 1962 <tibble> <lm> (Interc… 16.6 9.52 1.74 9.11e-2
6 Asia 1962 <tibble> <lm> log(gdp… 4.59 1.24 3.72 7.94e-4
7 Asia 1967 <tibble> <lm> (Interc… 19.8 9.05 2.19 3.64e-2
8 Asia 1967 <tibble> <lm> log(gdp… 4.50 1.15 3.90 4.77e-4
9 Asia 1972 <tibble> <lm> (Interc… 21.9 8.14 2.69 1.13e-2
10 Asia 1972 <tibble> <lm> log(gdp… 4.44 1.01 4.41 1.16e-4
# ℹ 110 more rowsMaking a plot with error bars in R
lm_data <- gapminder |>
nest(data = -c(continent, year)) |>
mutate(
fit = map(data, ~lm(lifeExp ~ log(gdpPercap), data = .x)),
tidy_out = map(fit, tidy)
) |>
unnest(cols = tidy_out) |>
select(-fit, -data)
lm_data# A tibble: 120 × 7
continent year term estimate std.error statistic p.value
<fct> <int> <chr> <dbl> <dbl> <dbl> <dbl>
1 Asia 1952 (Intercept) 15.8 9.27 1.71 0.0978
2 Asia 1952 log(gdpPercap) 4.16 1.25 3.33 0.00228
3 Asia 1957 (Intercept) 18.1 9.70 1.86 0.0720
4 Asia 1957 log(gdpPercap) 4.17 1.28 3.26 0.00271
5 Asia 1962 (Intercept) 16.6 9.52 1.74 0.0911
6 Asia 1962 log(gdpPercap) 4.59 1.24 3.72 0.000794
7 Asia 1967 (Intercept) 19.8 9.05 2.19 0.0364
8 Asia 1967 log(gdpPercap) 4.50 1.15 3.90 0.000477
9 Asia 1972 (Intercept) 21.9 8.14 2.69 0.0113
10 Asia 1972 log(gdpPercap) 4.44 1.01 4.41 0.000116
# ℹ 110 more rowsMaking a plot with error bars in R
lm_data <- gapminder |>
nest(data = -c(continent, year)) |>
mutate(
fit = map(data, ~lm(lifeExp ~ log(gdpPercap), data = .x)),
tidy_out = map(fit, tidy)
) |>
unnest(cols = tidy_out) |>
select(-fit, -data) |>
filter(term != "(Intercept)", continent != "Oceania")
lm_data# A tibble: 48 × 7
continent year term estimate std.error statistic p.value
<fct> <int> <chr> <dbl> <dbl> <dbl> <dbl>
1 Asia 1952 log(gdpPercap) 4.16 1.25 3.33 0.00228
2 Asia 1957 log(gdpPercap) 4.17 1.28 3.26 0.00271
3 Asia 1962 log(gdpPercap) 4.59 1.24 3.72 0.000794
4 Asia 1967 log(gdpPercap) 4.50 1.15 3.90 0.000477
5 Asia 1972 log(gdpPercap) 4.44 1.01 4.41 0.000116
6 Asia 1977 log(gdpPercap) 4.87 1.03 4.75 0.0000442
7 Asia 1982 log(gdpPercap) 4.78 0.852 5.61 0.00000377
8 Asia 1987 log(gdpPercap) 5.17 0.727 7.12 0.0000000531
9 Asia 1992 log(gdpPercap) 5.09 0.649 7.84 0.00000000760
10 Asia 1997 log(gdpPercap) 5.11 0.628 8.15 0.00000000335
# ℹ 38 more rowsMaking a plot with error bars in R
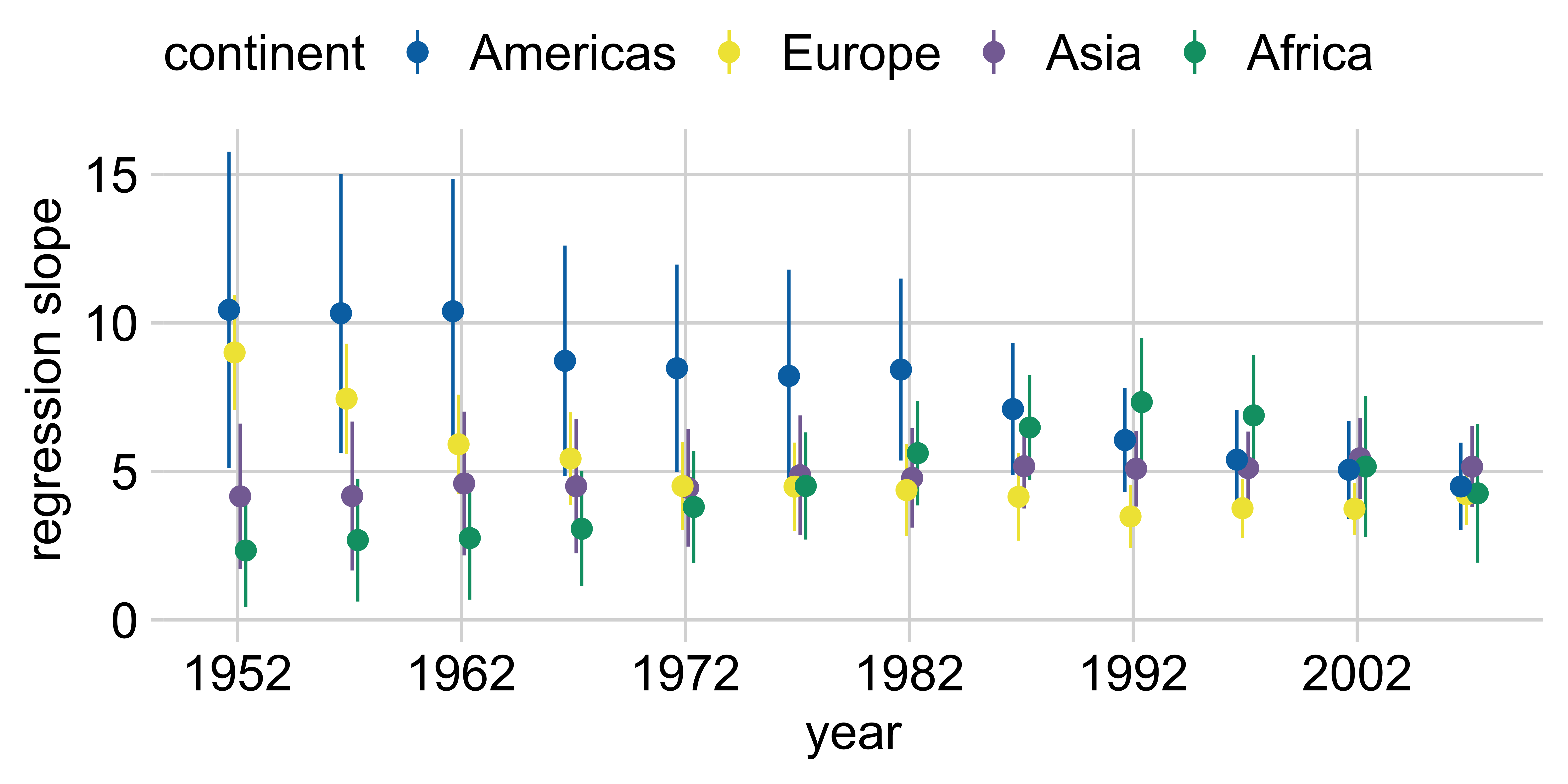
ggplot(lm_data) +
aes(
x = year, y = estimate,
ymin = estimate - 1.96*std.error,
ymax = estimate + 1.96*std.error,
color = continent
) +
geom_pointrange(
position = position_dodge(width = 1)
) +
scale_x_continuous(
breaks = gapminder |> distinct(year) |> pull(year)
) +
theme(legend.position = "top")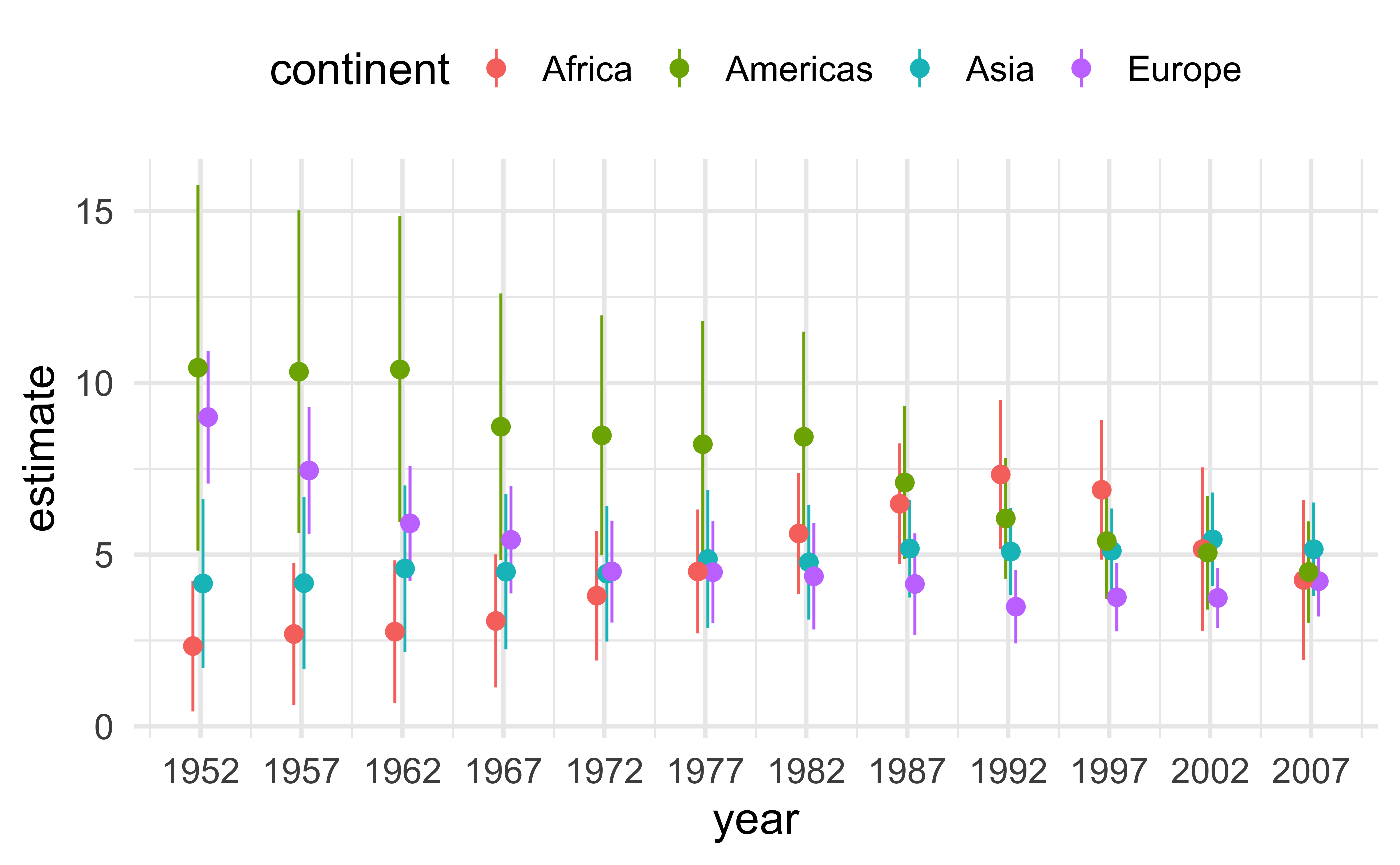
Data prep
For 1952 only:
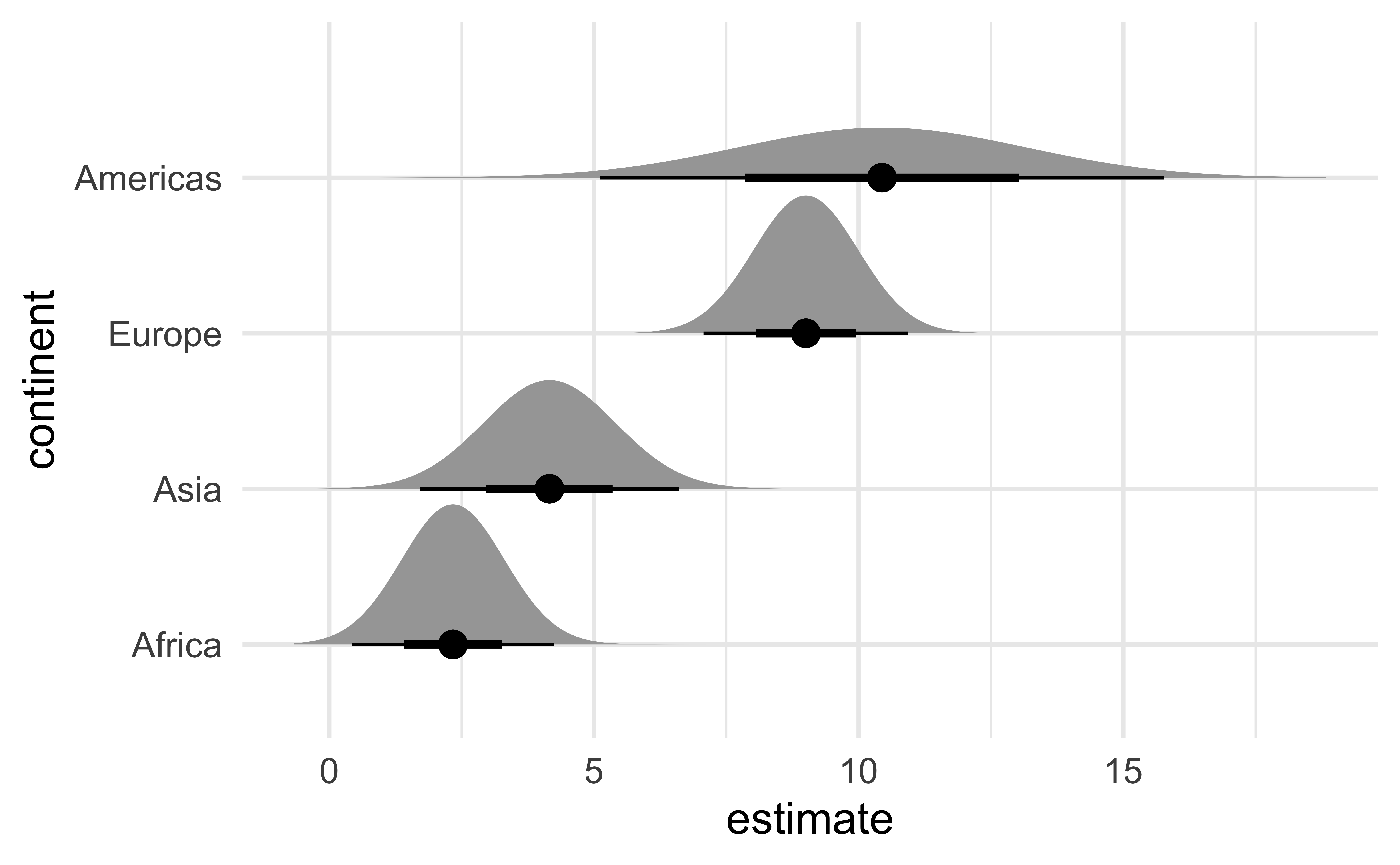
Half-eye
ggdist::stat_dist_halfeye():
Gradient interval
ggdist::stat_dist_gradientinterval():
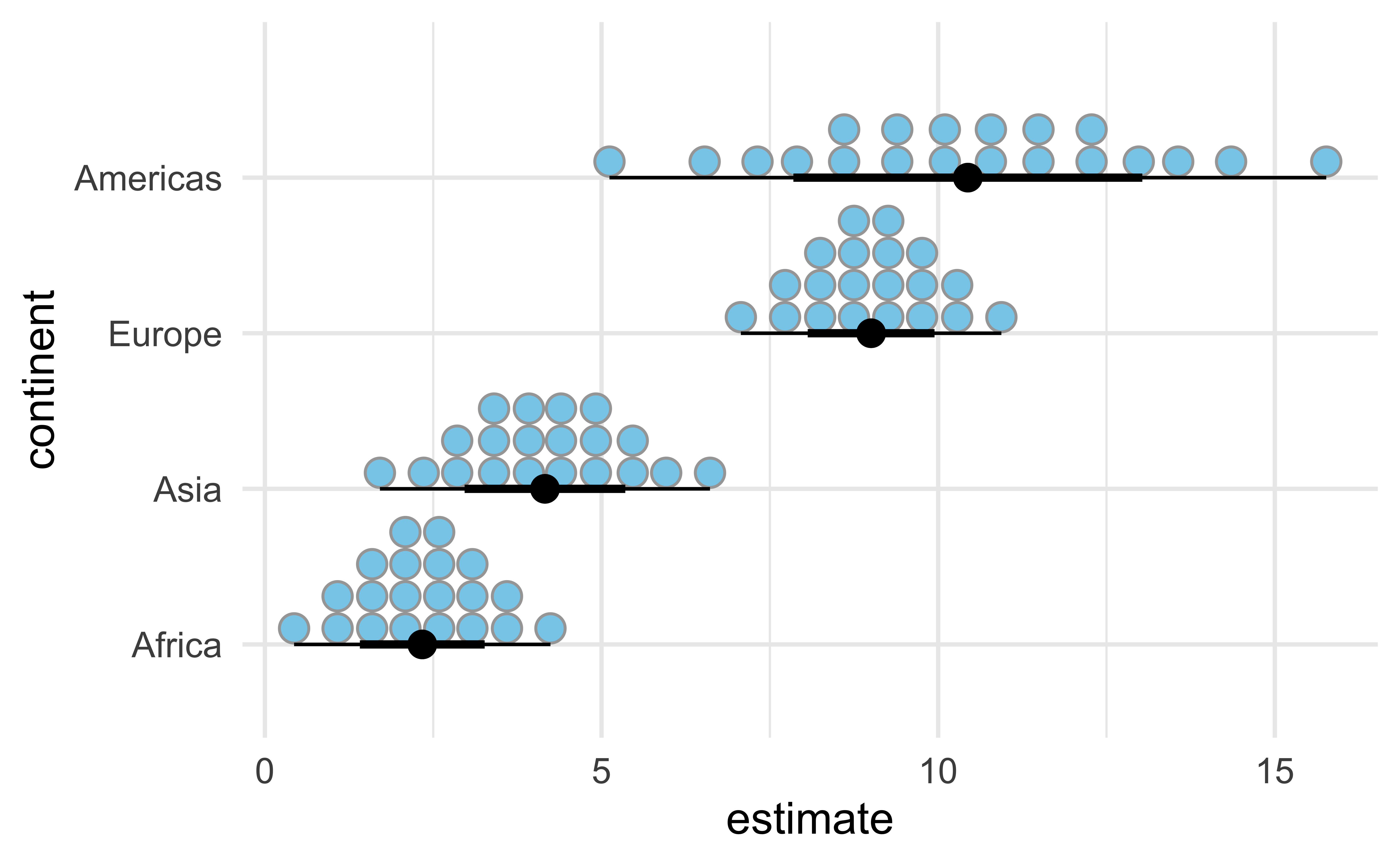
Dots interval
ggdist::stat_dist_dotsinterval():
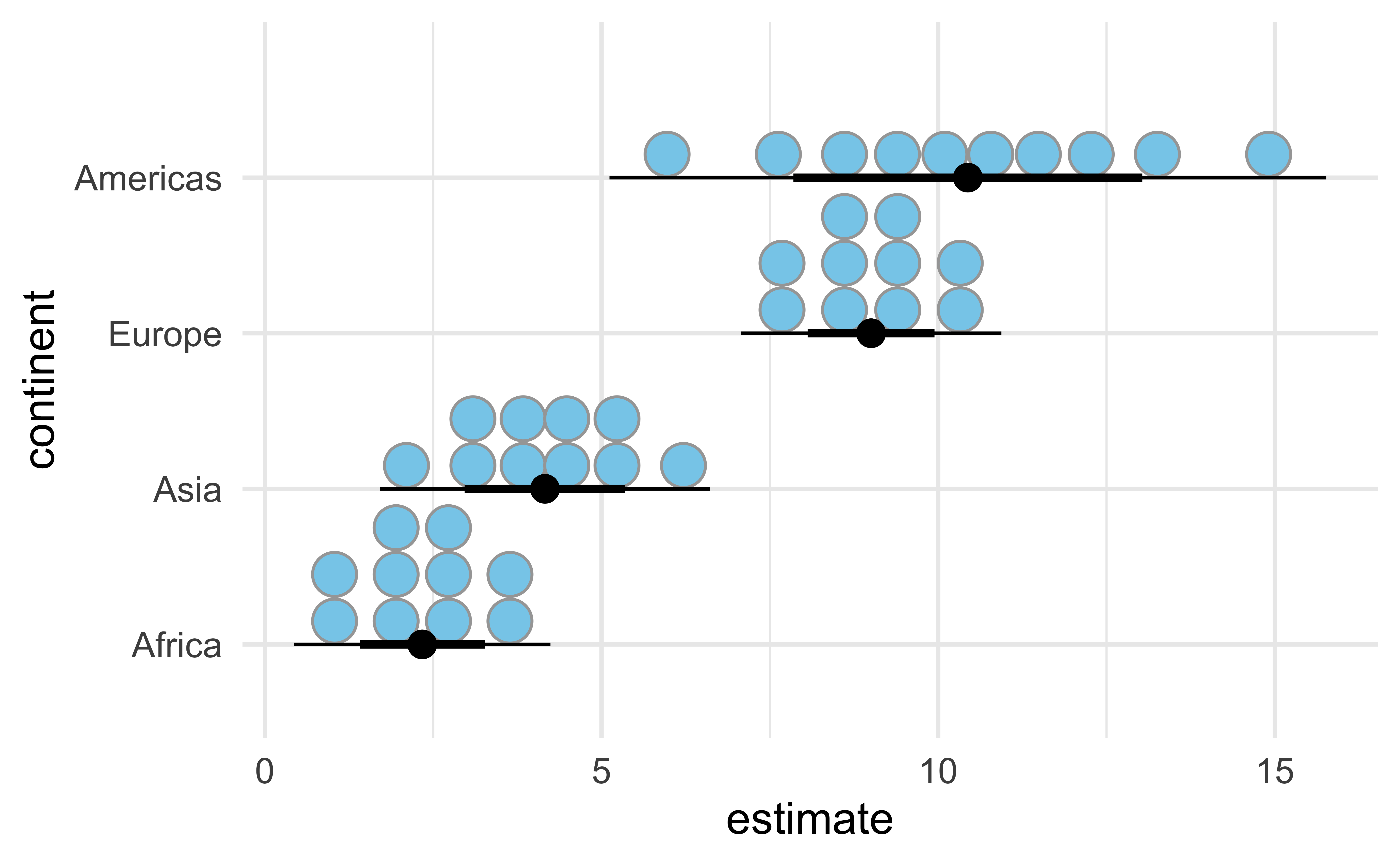
Dots interval
ggdist::stat_dist_dotsinterval():
Further reading and acknowledgements
- Acknowledgements: Slides from Visualizing uncertainty by Claus Wilke
- Further reading
- Fundamentals of Data Visualization: Chapter 16: Visualizing uncertainty
- Data Visualization—A Practical Introduction: Chapter 6.6: Grouped analysis and list columns
- Data Visualization—A Practical Introduction: Chapter 6.7: Plot marginal effects
- ggdist reference documentation: https://mjskay.github.io/ggdist/index.html
- ggdist vignette: Frequentist uncertainty visualization